Curso de Verão 2017

Teoria e Prática de Processamento de Sinais e Imagens

Processamento do Sinal de Voz

Ver também: https://fei.edu.br/~isanches/verao/curso_de_verao_2017.pdf

Ivandro Sanches

Depto. Eng. Elétrica

Centro Universitário FEI

Programação

Amostragem e quantização

Áudio

  • geração
  • importação/exportação
  • gravação

Processamento do áudio

  • segmentação
  • energia/taxa de cruzamentos por zero
  • convolução/filtragem
  • transformada discreta de Fourier

Visualização

  • sinal no tempo e em frequência
  • espectrograma

Produção da voz

  • pitch
  • formantes
  • vogais/consoantes

Percepção da voz

  • curvas de loudness
  • bandas críticas
  • mascaramento

Algumas aplicações e referências bibliográficas

Laboratório

  • introdução de eco, inversão no tempo, áudio estéreo
  • filtragem de ruído
  • energia e taxa de cruzamentos por zero
  • função de autocorrelação

Amostragem e quantização

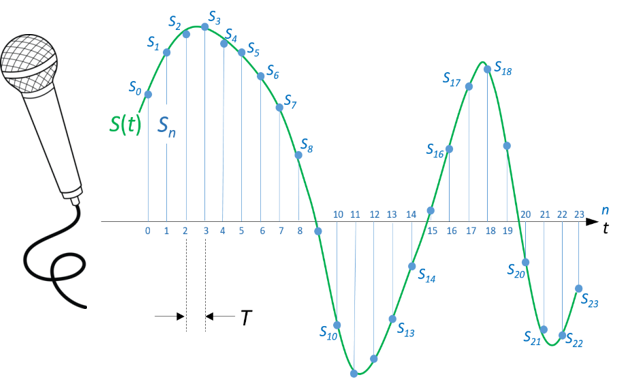
$T$ : período de amostragem, s

$f_s = \frac{1}{T}$ : frequência de amostragem, Hz

Exemplos $f_s$, kHz $T$, s
Áudio de CD 44 22.7 $\mu$s
Telefonia 8 125 $\mu$s
cabeçalho arquivo .wav
0010101001110101
0010101001110101
0010101001110101
...
0010101001110101

Resolução em número de bits

In [1]:
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
In [2]:
def requantiza(sinal, nbits, B):
  """
  Requantiza sinal amostrado originalmente com nbits
  no sinal y representado com B bits
    input:
        sinal: sinal original (assume-se media em torno de zero)
        nbits: no. de bits da amostragem original
        B: no. de bits da reamostragem
    output:
        y: sinal requantizado em B bits

  Exemplo:
  p = np.arange(-1,1,.1)
  y0 = requantiza(p, 32, 1)
  y1 = requantiza(p, 32, 2)
  y2 = requantiza(p, 32, 4)
  y3 = requantiza(p, 32, 8)

  IS-25jan2017
  """
  if B >= nbits: # nada a fazer
      y = sinal
      return y

  M = 2**(nbits-1)
  Q = 2**(B-1)
  if max(sinal) - min(sinal) < 2: # sinal normalizado
      sinal2 = sinal * M
      if max(sinal2) > M:
          print('Checar sinal');
          return Null;

  sinal2 = np.floor(sinal2);
  y = np.floor(sinal2/M*Q);
  y = y/Q;
  return y
In [3]:
p = np.arange(-1,1,.1)
n = np.arange(0,len(p))
y0 = requantiza(p, 32, 1)
y1 = requantiza(p, 32, 2)
y2 = requantiza(p, 32, 3)
y3 = requantiza(p, 32, 4)

#matplotlib.pylab.rcParams['figure.figsize'] = (12, 8)
f, axarr = plt.subplots(2, 2, figsize=(12,8))
axarr[0, 0].scatter(n, p, color='r', label='original')
axarr[0, 0].stem(n, y0, label='quantizado')
axarr[0, 0].set_title('Quantização me 1 bit')
axarr[0, 0].grid()
axarr[0, 0].legend(loc=2)
axarr[0, 1].scatter(n, p, color='r', label='original')
axarr[0, 1].stem(n, y1, label='quantizado')
axarr[0, 1].set_title('Quantização me 2 bits')
axarr[0, 1].grid()
axarr[0, 1].legend(loc=2)
axarr[1, 0].scatter(n, p, color='r', label='original')
axarr[1, 0].stem(n, y2, label='quantizado')
axarr[1, 0].set_title('Quantização me 3 bits')
axarr[1, 0].grid()
axarr[1, 0].legend(loc=2)
axarr[1, 0].set_xlabel('n')
axarr[1, 1].scatter(n, p, color='r', label='original')
axarr[1, 1].stem(n, y3, label='quantizado')
axarr[1, 1].set_title('Quantização me 4 bits')
axarr[1, 1].grid()
axarr[1, 1].legend(loc=2)
axarr[1, 1].set_xlabel('n')
# Fine-tune figure; hide x ticks for top plots and y ticks for right plots
plt.setp([a.get_xticklabels() for a in axarr[0, :]], visible=False)
plt.setp([a.get_yticklabels() for a in axarr[:, 1]], visible=False)
plt.show()

Taxa de Nyquist (mínima frequência de amostragem)

In [4]:
y = requantiza(p, 16, 2);
In [5]:
# geracao de forma de onda
fs = 44100  # freq de amostragem
T = 0.2     # duracao em segundos
t = np.arange(fs*T)/fs  # eixo do tempo
f1 = 90  # feq do sinal original

# signal original
y = np.cos(2*np.pi*f1*t)
plt.figure(figsize=(12,5))
plt.plot(t, y)
plt.title('tom em ' + str(f1) + ' Hz')
plt.xlabel('t, s')
plt.ylabel('y(t)')
plt.grid()
plt.show()
In [6]:
# frequência de amostragem de y(t)
f2 = 100
nf2 = np.floor(fs/f2) # no. amostras em 1/f2
# sinal y amostrado a f2, Hz
y2 = y[::nf2]
t2 = t[::nf2]

plt.figure(figsize=(12,5))
plt.plot(t, y)
plt.title('y(t)')
plt.xlabel('t, s')
plt.grid()
# sinal discreto no tempo
plt.stem(t2, y2, 'k')
plt.plot(t2, y2, 'g:')
plt.title('tom em ' + str(f1) + ' Hz amostrado a ' + str(f2) + ' Hz')
plt.show()
In [7]:
# sinal efetivamente obtido da amostragem errônea
plt.figure(figsize=(12,5))
n = range(len(y2))
plt.stem(n, y2, 'k')
plt.plot(n, y2, 'g:')
plt.title('aspecto do sinal amostrado: tom em ' + str(abs(f1-f2)) + ' Hz')
plt.xlabel('n')
plt.grid()
plt.show()

Áudio

Geração, reprodução, exportação, importação

Abaixo é apresentado um exemplo de geração de um tom em uma dada frequência.

Posteriormente, cria-se um sinal ruidoso, o qual é formado pelo tom gerado anteriormente e ruído gaussiano a uma determinada relação sinal-ruído a ser definida (SNR: signal-to-noise ratio)

In [8]:
# geração de tom na frequência f1
fs = 44100 # frequência de amostragem, Hz
f1 = 5000  # frequência do tom, Hz
T = 3      # duração em segundos
N = fs * T # número total de amostras
A = 0.8    # amplitude
n = np.arange(N) # índice das amostras
t = n/fs         # índice da escala de tempo
s = A * np.sin(2*np.pi*f1*t) # amostras do tom

# salvando tom em disco (exportação)
from scipy.io import wavfile
K = 2**15 - 1 # short: 16 bits
samples = np.floor(s*K)
samples = samples.astype(np.short)
fname = 'tom_' + str(f1) + 'Hz.wav'
wavfile.write(fname, fs, samples)

# leitura das amostras de arquivo de áudio em disco (importação)
rate, data = wavfile.read(fname)

# rate deve ser igual a fs e data igual a samples
print('Linha abaixo deve ser True')
print(rate == fs)
print('Linha abaixo deve ser zero')
print(np.max(np.abs(data-samples)))

Linha abaixo deve ser True
True
Linha abaixo deve ser zero
0
In [9]:
# reprodução de arquivo de áudio em disco
import IPython
IPython.display.Audio(fname)
Out[9]:
In [10]:
# reprodução de arquivo de áudio em disco (alternativa)
import winsound
winsound.PlaySound(fname, winsound.SND_FILENAME)

Cria-se agora ruído gaussiano branco de mesmo tamanho do sinal s

In [11]:
np.random.seed(0)
r = np.random.randn(N)
In [12]:
# constata-se que a média é próxima de zero e o desvio padrão próximo de 1
print('Ruído:')
print('\tmédia         = {0:9.5f}'.format(np.mean(r)))
print('\tdesvio padrão = {0:9.5f}'.format(np.std(r)))

Ruído:
	média         =   0.00368
	desvio padrão =   0.99777
In [13]:
# retira-se a média do ruído
r = r - np.mean(r)
print('Ruído:')
print('\tmédia         = {0:9.5f}'.format(np.mean(r)))
print('\tdesvio padrão = {0:9.5f}'.format(np.std(r)))

Ruído:
	média         =   0.00000
	desvio padrão =   0.99777
In [14]:
# cálculo da energia do tom e da energia do ruído
es = np.sum(s*s)
print('energia do tom: {0:9.5f}'.format(es))
er = np.sum(r*r)
print('energia do ruído: {0:9.5f}'.format(er))

energia do tom: 42336.00000
energia do ruído: 131709.28113

Relação sina-ruído corrente:

In [15]:
snr = 10 * np.log10(es/er)
print(snr)

-4.92906556855
In [16]:
SNR = 5
print('Relação sinal-ruído desejada = {0:.1f}'.format(SNR))

Relação sinal-ruído desejada = 5.0
In [17]:
k = 10**(SNR/10) # deseja-se que es/er seja k, logo:
r = r * (es / (er * k))**0.5
In [18]:
er = np.sum(r*r)
print('energia ajustada do ruído: {0:9.5f}'.format(er))

energia ajustada do ruído: 13387.81870

Relação sinal-ruído corrente e ajustada para o valor desejado SNR

In [19]:
snr = 10 * np.log10(es/er)
print(snr)

5.0

Constituição do sinal ruidoso x

In [20]:
x = s + r
In [21]:
ind = np.arange(100, 200)
plt.figure(figsize=(12,5))
plt.plot(n[ind], s[ind], 'b', n[ind], x[ind], 'r')
plt.legend(('original', 'ruidoso'), loc='best')
plt.xlabel('n')
plt.grid()
plt.show()

Geracao de tom de frequencia variavel linearmente

In [22]:
def genlin(td, fi, ff, fs):
    """
    Geracao de tom de frequencia variavel linearmente
    sinal = genlin(td, fi, ff, fs)
    td: duracao do tom em segundos, ex. 10 s
    fi: freq. inicial (fi < fs/2), ex. 100 Hz
    ff: freq. final (ff < fs/2), ex. 12000 Hz
    fs: freq. de amostragem, ex. 44100 Hz
    sinal: sinal gerado
    """
    t = np.arange(0,1,1.0/(td*fs))
    if fi <= ff:
        freqlin = fi + (ff-fi)*t
    else:
        freqlin = fi - (fi-ff)*t
    sinal = freqgen(freqlin, fs) # funcao definida a seguir
    return sinal
In [23]:
def freqgen(fr, fs):
    """
    Geracao de tom de frequencia variavel dada por fr
    Amplitude unitária e gerado via sin()
    """
    fr = fr*2*np.pi/fs # normalizacao para rad/s
    phi = np.cumsum(fr) # soma acumulada
    sinal = np.sin(phi)
    return sinal

Breve explicação de freqgen()

Se uma forma de onda $x(t)$ é definida como $$ x(t) = \sin ( \phi(t)) $$

então, sua frequência instantânea é definida pela taxa da fase $$ \omega(t) = \frac{d \, \phi(t)}{d \, t} \rightarrow f(t) = \frac{1}{2 \pi} \, \frac{d \, \phi(t)}{d \, t} \; . $$

Daí o uso de np.cumsum() em freqgen().

In [24]:
fs = 44100
sinal1 = genlin(4, 500, 15000, fs)

# salvando em disco sob fname
fname = 'genlin.wav'
K = 2**15 - 1 # short: 16 bits
samples = np.floor(sinal1*K)
samples = samples.astype(np.short)
wavfile.write(fname, fs, samples)
In [25]:
# reprodução de arquivo de áudio em disco
import IPython
IPython.display.Audio(fname)
Out[25]:
In [26]:
# reprodução de arquivo de áudio em disco (alternativa)
import winsound
winsound.PlaySound(fname, winsound.SND_FILENAME)
In [27]:
# espectrograma
#from scipy.io import wavfile
#fs, samples = wavefile.read(fname)
nfft = 1024
plt.figure(figsize=(10,8))
opxx, freqs, bins, im = plt.specgram(samples, nfft, fs, noverlap=7*nfft/8,
                                     cmap=plt.cm.gist_stern)
plt.xlabel('tempo, s')
plt.ylabel('frequência, Hz')
axes = plt.gca()
axes.set_ylim([0, fs/2])
plt.show()

Geracao de tom de frequencia variavel exponencialmente

In [28]:
def genexp(td, c, fi, ff, fs):
    """
    Geracao de tom de frequencia variavel exponencialmente
    sinal = genexp(td, c, fi, ff, fs)
        td: duracao do tom em segundos, ex. 10 s
        c: grau de curvatura, (c >= 0), ex. 1
        fi: freq. inicial (fi < fs/2), ex. 100 Hz
        ff: freq. final (ff < fs/2), ex. 12000 Hz
        fs: freq. de amostragem, ex. 44100 Hz
        sinal: sinal gerado
    """
    x = np.arange(0, 1, 1./(td*fs))
    m = np.exp(c) # m constante de warping
    M = np.exp(m)
    if fi <= ff:
        freqexp = fi + (np.exp(m*x)-1)/(M-1)*(ff-fi)
    else:
        freqexp = ff + (np.exp(m*x)-1)/(M-1)*(fi-ff)
        freqexp = freqexp[-1::-1]
    sinal = freqgen(freqexp, fs)
    return sinal
In [29]:
fs = 44100;
sinal2 = genexp(4, 1, 500, 15000, fs);

# salvando em disco sob fname
fname = 'genexp.wav'
K = 2**15 - 1 # short: 16 bits
samples = np.floor(sinal2*K)
samples = samples.astype(np.short)
wavfile.write(fname, fs, samples)
In [30]:
# reprodução de arquivo de áudio em disco
import IPython
IPython.display.Audio(fname)
Out[30]:
In [31]:
# reprodução de arquivo de áudio em disco (alternativa)
import winsound
winsound.PlaySound(fname, winsound.SND_FILENAME)
In [32]:
# espectrograma
#from scipy.io import wavfile
#fs, samples = wavefile.read(fname)
nfft = 1024
plt.figure(figsize=(10,8))
opxx, freqs, bins, im = plt.specgram(samples, nfft, fs, noverlap=7*nfft/8,
                                     cmap=plt.cm.gist_stern)
plt.xlabel('tempo, s')
plt.ylabel('frequência, Hz')
axes = plt.gca()
axes.set_ylim([0, fs/2])
plt.show()
In [33]:
fs = 44100
sinal3 = 0.5*sinal1 + 0.5*sinal2;
# salvando em disco sob fname
fname = 'linexp.wav'
K = 2**15 - 1 # short: 16 bits
samples = np.floor(sinal3*K)
samples = samples.astype(np.short)
wavfile.write(fname, fs, samples)
nfft = 1024
plt.figure(figsize=(10,8))
opxx, freqs, bins, im = plt.specgram(samples, nfft, fs, noverlap=7*nfft/8,
                                     cmap=plt.cm.gist_stern)
# ou, diretamente com sinal3:
# opxx, freqs, bins, im = plt.specgram(sinal3, nfft, fs, noverlap=7*nfft/8,
#                                      cmap=plt.cm.gist_stern)
plt.xlabel('tempo, s')
plt.ylabel('frequência, Hz')
axes = plt.gca()
axes.set_ylim([0, fs/2])
plt.show()

Criação de áudio estéreo

In [34]:
fs = 44100;
canalesquerdo = genexp(4, 1, 500, 15000, fs);
canaldireito = genexp(4, 1, 15000, 500, fs);
In [35]:
estereo = np.vstack((canalesquerdo, canaldireito))
print('shape antes :', estereo.shape)
estereo = estereo.T
print('De: https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.io.wavfile.write.html')
print('To write multiple-channels, use a 2-D array of shape (Nsamples, Nchannels).')
print('shape depois:', estereo.shape)
print(type(estereo))
# salvando em disco sob fname
fname = 'estereo.wav'
K = 2**15 - 1 # short: 16 bits
samples = np.floor(estereo*K)
samples = samples.astype(np.short)
print('shape samples:', estereo.shape)
wavfile.write(fname, fs, samples)

shape antes : (2, 176400)
De: https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.io.wavfile.write.html
To write multiple-channels, use a 2-D array of shape (Nsamples, Nchannels).
shape depois: (176400, 2)
<class 'numpy.ndarray'>
shape samples: (176400, 2)
In [36]:
# reprodução de arquivo de áudio em disco
import IPython
IPython.display.Audio(fname)
Out[36]:

Gravação de áudio

A gravação (criação) de arquivo de áudio (por exemplo .wav) pode ser feita via algum programa/aplicativo externo e sua posterior importação para o ambiente python.

Exemplos de programas para manipulação de áudio:

a. Wavesurfer

b. Audacity

c. SFS

d. SonicVisualizer

Segmentação

Como o sinal de voz apresenta trechos com características bastante diversas, seu processamento precisa ser feito por segmentos. O ideal é que cada trecho com características semelhantes pudesse ser tratado individualmente. Como isso não é possível, o sinal de voz (e de áudio) é processado por segmentação.

O tamanho de cada segmento não pode ser muito pequeno, pois a informação contida não é suficiente, e também não pode ser muito grande, quando trechos com características distintas seriam tratados em conjunto.

Dessa forma há um compromisso e o tipo de processamento e sua finalidade acabam por sugerir tamanhos adequados para segmentos.

Por exemplo, em reconhecimento de fala é usual que segmentos tenham tamanhos de 20 ms. Adicionalmente, ocorre sobreposição entre segmentos sendo analidados.

Concretamente, suponha um sinal com duração de 10 s. Caso esse sinal seja analisado por segmentos de 25 ms aplicados a cada 10 ms, qual é o número total de segmentos a ser processado?

Têm-se então as variáveis envolvidas:

$T$ = 10 s, a duração total do sinal

$S$ = 0.025 s, o tamanho de um segmento

$dS$ = 0.010 s, o tempo entre deslocamentos dos segmentos

Chega-se que o número de segmentos, $M$, resulta em

$$ M = \frac{T – S}{dS} + 1 $$

ou

$$ M = \frac{T – S + dS}{dS} $$

Substituindo os valores $$ M = \frac{10 – 0.025 + 0.010}{0.010} = 998.5 $$

A parte decimal deve ser descartada pois não se processam trechos com duração menor do que um segmento.

Portanto, neste exemplo fictício, resulta em um total de 998 segmentos.

Energia

Uma informação importante sobre um sinal é o comportamento da energia ao longo do tempo.

Dado um segmento de duração $S$ de um sinal que foi amostrado à frequência de amostragem $f_s$ , é fácil calcularmos o tamanho em amostras desse segmento.

Seja $N$ o número de amostras em um segmento de duração $S$, em segundos, extraído de um sinal que foi amostrado à taxa $f_s$ , em Hz. Tem-se que

$$ N = S \, f_s $$

Sejam então as $N$ amostras contidas no segmento de duração $S$

$$ s_0, s_1, s_2, \ldots, s_{N-1} $$

A energia desse segmento é dada por:

$$ E = s_0^2 + s_1^2 + s_2^2 + \ldots + s_{N-1}^2 $$

ou, ainda, de forma mais compacta

$$ E = \sum_{i=0}^{N-1} s_i^2 $$

Taxa de cruzamentos por zero

Uma informação relativamente simples de ser computada e que dá uma ideia do conteúdo em frequência do sinal sendo analidado é a taxa de cruzamentos por zero (TCZ).

Dado um segmento com $N$ amostras, a taxa de cruzamentos por zero, $Z$, pode ser computada pela expressão

$$ Z = \frac{1}{2(N-1)} \sum_{i=1}^{N-1} |\text{sign}(s_i) - \text{sign}(s_{i-1})| $$

Onde

$$ \text{sign}(s_i) = \left\{ \begin{array}{rl} 1, & \text{se } s_i \geq 0\\ -1, & \mbox{se } s_i < 0 \end{array} \right. $$

Vê-se que $$ 0 \leq Z \leq 1 $$

Quanto mais próximo $Z$ for de 1, maior o conteúdo em frequência do segmento. Note que quando $Z$ = 0, o sinal não cruzou o eixo.

Vê-se que essa grandeza é muito sensível a eventuais niveis DC presentes no sinal. Dessa forma, recomenda-se que se retire o nível médio do sinal ou que seja filtrado adequadamente.

Energia e TCZ

Seja o sinal de áudio seis.wav. A figura ilustra o comportamento da energia, $E$, e da TCZ, $Z$, desse sinal em segmentos de 20 ms a cada 10 ms. O aspecto geral dessas curvas é o esperado?

In [37]:
from scipy.io import wavfile
fname = '../seis.wav'
fsseis, seis = wavfile.read(fname)
seis = seis - np.mean(seis); # agora sem nivel medio
T = len(seis)/fsseis
S = 20e-3
dS = 10e-3
M = int(np.floor((T-S+dS)/dS))
N = int(S * fsseis)
N1 = N - 1
dN = int(dS * fsseis)
E = np.zeros((M, 1))
Z = np.zeros((M, 1))
ind = np.arange(N, dtype=int)
for i in range(M):
    s = seis[ind]
    E[i] = np.sum(s*s)
    Z[i] = np.sum(np.abs(np.sign(s[1:])-np.sign(s[:-1])))/(2*N1)
    ind = ind + dN
In [38]:
f, axarr = plt.subplots(3, 1, figsize=(12,15))
t = np.arange(len(seis))/fsseis
n = range(len(E))

axarr[0].plot(t, seis)
axarr[0].set_title('seis.wav')
axarr[0].set_xlabel('t, s')
axarr[0].set_ylabel('amplitude')
axarr[0].axis('tight')
axarr[0].grid()

axarr[1].plot(n, E, 'g')
axarr[1].set_ylabel('E')
axarr[1].set_xlabel('n, segmento de 1 a' + str(M) )
axarr[1].axis('tight')
axarr[1].grid()

axarr[2].plot(n, Z, 'r')
axarr[2].set_ylabel('Z')
axarr[2].set_xlabel('n, segmento de 1 a' + str(M) )
axarr[2].axis('tight')
axarr[2].grid()
plt.show()

Convolução

Seja uma sequência discreta $x(n)$ ou $x[n]$ ou $x_n$. Seja um sistema linear invariante no tempo cuja resposta ao impulso é $h(n)$. A saída desse sistema, $y(n)$, dá-se pela convolução entre $x(n)$ e $h(n)$:

$$ y(n) = h(n) \; * \; x(n) $$

A operação é comutativa:

$$ y(n) = x(n) \; * \; h(n) $$

Graficamente:

Explicitamente, a computação das amostras de saída dá-se pela expressão da convolução discreta:

$$ y(n) = \sum_{i=-\infty}^\infty h(i) \; x(n-i) $$

O módulo numpy provê a função de convolução

y = numpy.convolve(h, x)

No domínio da frequência (propriedade da transformada de Fourier discreta no tempo):

$$ Y(e^{j \, \omega}) = H(e^{j \, \omega}) \; X(e^{j \, \omega}) $$

Filtragem

Quando $h(n)$ corresponde à resposta ao impulso de um filtro digital, a convolução corresponde a um processo de filtragem e a saída desse processo pode ser obtida por:

y = numpy.convolve(h, x)

ou, com o uso do módulo scipy:

y = scipy.signal.lfilter(h, 1, x)

Vamos a seguir ilustar o projeto de um filtro digital. Nesse projeto simplificado, o resultado será a resposta ao impulso finita h, ou os coeficientes a e b que caracterizam o filtro, e que nos permitirá o processo de filtragem para uma entrada x qualquer.

Posteriormente, vamos ilustrar o projeto de um filtro digital que possui resposta ao impulso infinita. Neste caso, o projeto retornará 2 vetores, a e b, que utilizaremos no processo de filtragem da seguinte forma:

y = scipy.signal.lfilter(b, a, x)

Projeto de um filtro digital de resposta finita ao impulso.

Dados do projeto:

frequência de amostragem: 44100 Hz

frequência de corte inferior: 4900 Hz

frequência de corte superior: 5100 Hz

ordem do filtro: 200

In [39]:
from scipy import signal
# projeto do filtro, h
fs = 44100 # freq. amostragem
fb = 4900  # freq. baixa/inferior
fa = 5100  # freq. alta/superior
N = 200    # ordem
h = signal.firwin(N+1, [fb, fa], nyq=fs/2, pass_zero=False)
W, H = signal.freqz(h, 1)
F = W * fs/2/np.pi
fig = plt.figure(figsize=(12,10))
plt.title('Resposta em  frequência')
ax1 = fig.add_subplot(111)
plt.plot(F, 20 * np.log10(abs(H)), 'b')
plt.ylabel('Amplitude [dB]', color='b')
plt.xlabel('Frequência [Hz]')
ax2 = ax1.twinx()
fase = np.unwrap(np.angle(H))
plt.plot(F, fase, 'g:')
plt.ylabel('Fase (radianos)', color='g')
plt.grid()
plt.axis('tight')
plt.show()

Aplicação do filtro projetado

Lembrando que o sinal x é a senoide de 5 kHz mais ruído gaussiano a 5 db de SNR. O sinal y é o sinal x filtrado pelo filtro projetado anteriormente. Note que após o transitório inicial, que é da ordem do filtro, praticamente se obtém s, a senoide original de 5 kHz (quase sem ruído)

In [40]:
f, axarr = plt.subplots(2, 1, figsize=(8, 10))
ind1 = range(150, 501)
axarr[0].plot(ind1, x[ind1])
axarr[0].set_title('x')
axarr[0].set_ylabel('amplitude')
axarr[0].set_xlabel('n')
axarr[0].axis('tight')
axarr[0].grid()

# filtragem
ind2 = range(1000)
#y = signal.filtfilt(h, 1, x[ind2])
y = signal.lfilter(h, 1, x[ind2])

axarr[1].plot(ind1, y[ind1])
axarr[1].set_title('y')
axarr[1].set_ylabel('amplitude')
axarr[1].set_xlabel('n')
axarr[1].axis('tight')
axarr[1].grid()

plt.show()

Projeto de um filtro digital de resposta infinita ao impulso.

Dados do projeto:

frequência de amostragem: 44100 Hz

frequência de corte inferior: 4900 Hz

frequência de corte superior: 5100 Hz

ordem do filtro Butterworth: 10

In [41]:
# projeto do filtro, [b, a]
fs = 44100 # freq. amostragem
fb = 4900  # freq. baixa/inferior
fa = 5100  # freq. alta/superior
N = 5      # ordem/2
nyq = fs/2
b, a = signal.butter(N, [fb/nyq, fa/nyq], 'bandpass')
W, H = signal.freqz(b, a)
F = W * fs/2/np.pi
fig = plt.figure(figsize=(12,10))
plt.title('Resposta em  frequência')
ax1 = fig.add_subplot(111)
plt.plot(F, 20 * np.log10(abs(H)), 'b')
plt.ylabel('Amplitude [dB]', color='b')
plt.xlabel('Frequência [Hz]')
ax2 = ax1.twinx()
fase = np.unwrap(np.angle(H))
plt.plot(F, fase, 'g:')
plt.ylabel('Fase (radianos)', color='g')
plt.grid()
plt.axis('tight')
plt.show()

Aplicação do filtro projetado

In [42]:
f, axarr = plt.subplots(2, 1, figsize=(8, 10))
axarr[0].plot(ind1, x[ind1])
axarr[0].set_title('x')
axarr[0].set_ylabel('amplitude')
axarr[0].set_xlabel('n')
axarr[0].axis('tight')
axarr[0].grid()

# filtragem

#y = signal.filtfilt(b, a, x[ind2])
y = signal.lfilter(b, a, x[ind2])

axarr[1].plot(ind1, y[ind1])
axarr[1].set_title('y')
axarr[1].set_ylabel('amplitude')
axarr[1].set_xlabel('n')
axarr[1].axis('tight')
axarr[1].grid()

plt.show()

Transformada Discreta de Fourier

A transformada discreta de Fourier (Discrete Fourier Transform, DFT) converte uma sequência finita no tempo em sua correspondente versão em frequência. Isto é, a DFT é a representação no domínio da frequência da sequência original de entrada.

As expressões de análise e síntese, para a sequência original $x(n), n = 0, 1, \ldots, N-1$, são:

Análise: $$ X(k) = \sum_{n=0}^{N-1} x(n) \; e^{-j \frac{2\,\pi}{N} k \, n}, \hspace{1cm} k = 0, 1, 2, \dots, N-1 $$ Síntese: $$ x(n) = \sum_{k=0}^{N-1} X(k) \; e^{\, j \frac{2\,\pi}{N} k \, n}, \hspace{1cm} n = 0, 1, 2, \dots, N-1 $$

Indica-se o par de transformadas na forma $$ x(n) \leftrightarrow X(k) $$

Exemplo em Python:

>>> from scipy.fftpack import fft, ifft
>>> x1 = np.arange(5)
>>> X1 = fft(x1)
>>> x2 = ifft(X1)
>>> np.allclose(x1, x2, atol=1e-15)  # dentro da precisão numérica
True
In [43]:
from scipy.fftpack import fft, ifft
x1 = np.arange(5)
X1 = fft(x1)
x2 = ifft(X1)
np.allclose(x1, x2, atol=1e-15)  # dentro da precisão numérica
Out[43]:
True

Geralmente o sinal no tempo, $x(n)$, é uma sequência real. Normalmente a sequência transformada, $X(k)$, é complexa. Portanto, note abaixo o uso da função abs() nas transformadas de sequências vistas anteriormente.

In [44]:
# x é a senoide com ruído
# adicionado a 5 dB de SNR
X = fft(x);
Xa = np.abs(X);

f, axarr = plt.subplots(2, 1, figsize=(8,10))

axarr[0].plot(x)
axarr[0].set_title('x')
axarr[0].set_xlabel('n')
axarr[0].axis('tight')
axarr[0].grid()

axarr[1].plot(Xa)
axarr[1].set_title('abs(fft(x))')
axarr[1].set_xlabel('k')
axarr[1].axis('tight')
axarr[1].grid()

plt.show()

Vamos enxergar melhor o que está ocorrendo nas figuras anteriores ao melhorar a visualização de seu conteúdo. Assim, vamos:

  1. olhar um pequeno trecho em detalhe do sinal x
  2. converter o eixo x da DFT para Hz e mostrar apenas a primeira metade, já que a segunda metade é a imagem Hermitiana da primeira (isto é, as partes reais são idênticas e as partes imaginárias têm o sinal trocado)
In [45]:
# trecho de x
ind = range(500, 601)
f, axarr = plt.subplots(2, 1, figsize=(8,10))
axarr[0].plot(ind, x[ind])
axarr[0].set_title('x')
axarr[0].set_xlabel('n')
axarr[0].axis('tight')
axarr[0].grid()

# eixo da DFT em Hz
fs = 44100
N = len(x)
Xb = Xa / N
freq = np.arange(0, N) / N * fs;
ind = range(int(N/2));
axarr[1].plot(freq[ind], Xb[ind])
axarr[1].set_title('abs(fft(x))')
axarr[1].axis('tight')
axarr[1].grid()
msg = 'aproximadamente 0.4, que é a metade da\n' +\
      'amplitude do sinal original (sem ruído)'
axarr[1].annotate(msg, xy=(5200, 0.395), xytext=(8000, 0.3),
                  arrowprops=dict(facecolor='red', shrink=0.01))
plt.show()

sinal1, visto anteriormente, tem sua frequência saindo de 500 Hz e chegando a 15 kHz de forma linear. Vamos analisar 2 trechos desse sinal, no início e no fim. Cada trecho terá o comprimento de N = 512 amostras. Note que a DFT revela a concentração de energia em 500 Hz e a amplitude de (2 $\times$ 0.5 = 1.0)

In [46]:
# trecho inicial de sinal1 (primeiras N amostras)
N = 512
ind = np.arange(N)
t = ind/fs
s1 = sinal1[ind]
S1 = np.abs(fft(s1))

f, axarr = plt.subplots(2, 1, figsize=(8,10))
axarr[0].plot(t, s1)
axarr[0].set_title('s1')
axarr[0].set_xlabel('t, s')
axarr[0].axis('tight')
axarr[0].grid()

# eixo da DFT em Hz
S_1 = S1[0:N//2] / N
freq = np.arange(0, N//2) / N * fs;
axarr[1].plot(freq, S_1)
axarr[1].set_title('abs(fft(s1))')
axarr[1].set_xlabel('f, Hz')
axarr[1].axis('tight')
axarr[1].grid()
msg = 'aproximadamente 0.5, que é a\n' +\
      ' metade da amplitude do sinal1'
axarr[1].annotate(msg, xy=(550, 0.49), xytext=(3000, 0.3),
                  arrowprops=dict(facecolor='red', shrink=0.01))
msg = 'aproximadamente 500 Hz, que é a\n' +\
      'frequência inicial do sinal'
axarr[1].annotate(msg, xy=(520, 0.01), xytext=(3000, 0.2),
                  arrowprops=dict(facecolor='red', shrink=0.01))
plt.show()

Análise do trecho final de N = 512 amostras do sinal1, quando sua frequência atinge 15 kHz.

In [47]:
# trecho final de sinal1 (ultimas N amostras)
N = 512
ind = np.arange(N) + len(sinal1) - N
t = ind/fs
s2 = sinal1[ind]
S2 = np.abs(fft(s2))

f, axarr = plt.subplots(2, 1, figsize=(8,10))
axarr[0].plot(t, s2)
axarr[0].set_title('s2')
axarr[0].set_xlabel('t, s')
axarr[0].axis('tight')
axarr[0].grid()

from matplotlib.patches import Ellipse

ellipse = Ellipse(xy=(3.994, 0.5), width=0.001, height=0.22, 
                        edgecolor='r', fill=False, lw=2, ls='dashed')
axarr[0].add_patch(ellipse)
axarr[0].annotate('', xy=(3.9945, 0.43), xytext=(3.995, 0.1),
                  arrowprops=dict(facecolor='red', shrink=0.01))
msg = ' efeitos/artefatos devidos à \n' +\
      ' frequência de amostragem ser \n' +\
      ' finita '
bbox_props = dict(fc=(.85, .85, .85), ec='b')
axarr[0].text(3.995, -0.1, msg, bbox=bbox_props)

# eixo da DFT em Hz
S_2 = S2[0:N//2] / N
freq = np.arange(0, N//2) / N * fs;
axarr[1].plot(freq, S_2)
axarr[1].set_title('abs(fft(s2))')
axarr[1].set_xlabel('f, Hz')
axarr[1].axis('tight')
axarr[1].grid()
msg = 'aproximadamente 15000 Hz,\nque é a' +\
      'frequência\nfinal do sinal'
axarr[1].annotate(msg, xy=(15000, 0.01), xytext=(5500, 0.22),
                  arrowprops=dict(facecolor='red', shrink=0.01))
f.tight_layout()
plt.show()

Espectrograma

O espectrograma combina os dois tipos de gráficos vistos nas células anteriores em um único gráfico. Usualmente representa-se o tempo ao longo do eixo x, a frequência ao longo do eixo y e a amplitude/intensidade como a cor do ponto (x,y). Como visto anteriormente, abaixo é ilustrado o espctrograma do sinal1

In [48]:
# espectrograma
#from scipy.io import wavfile
#fs, samples = wavefile.read(fname)
nfft = 1024 # pontos para FFT
plt.figure(figsize=(10,8))
opxx, freqs, bins, im = plt.specgram(
      sinal1, # amostras do sinal
      nfft,   # pontos para FFT
      fs,     # freq. amostragem
      noverlap=7*nfft/8, # sobreposição
      cmap=plt.cm.gist_stern) # colormap
plt.xlabel('tempo, s')
plt.ylabel('frequência, Hz')
axes = plt.gca()
axes.set_ylim([0, fs/2])
plt.show()

Espectrograma do sinal de voz no arquivo seis.wav

Note o limite no valor da escala de frequência: 4 kHz. Esse valor corresponde à metade da frequência de amostragem do sinal sendo analisado. Neste caso, $f_s$ = 8 kHz.

In [49]:
# espectrograma
#from scipy.io import wavfile
#fs, samples = wavefile.read(fname)
nfft = 256 # pontos para FFT
win = np.hamming(nfft)
plt.figure(figsize=(10,8))
opxx, freqs, bins, im = plt.specgram(
      seis,   # amostras do sinal
      nfft,   # pontos para FFT
      fsseis, # freq. amostragem
      window = win,        # janela
      noverlap = 7*nfft/8, # sobreposição
      pad_to = 2*nfft,     # tamanho com zero-padding
      cmap=plt.cm.gist_stern) # colormap
plt.xlabel('tempo, s')
plt.ylabel('frequência, Hz')
axes = plt.gca()
axes.set_ylim([0, fsseis/2])
plt.show()

Pitch

Pitch, $F_0$, ou frequência fundamental, é a frequência de vibração das cordas vocais. Valores baixos, entre 85 e 180 Hz, são frequentes no sexo masculino (adulto em fala normal). Valores femininos podem variar de 165 a 255 Hz. Crianças e, principalmente bebês, podem atingir valores acima de 300 Hz.

Na figura, estima-se um período com duração de cerca de 0.008 s, equivalendo ao pitch $$ F_0 = \frac{1}{0.008} = 125 \text{Hz.} $$

Esse valor sugere um locutor do sexo masculino.

In [50]:
f, axarr = plt.subplots(3, 1, figsize=(12,15))
t = np.arange(len(seis))/fsseis

axarr[0].plot(t, seis)
axarr[0].set_title('seis.wav')
axarr[0].axis('tight')

ind = range(4800, 6401)
axarr[1].plot(t[ind], seis[ind])
axarr[1].axis('tight')

ind = (t>0.68) & (t<0.72)
axarr[2].plot(t[ind], seis[ind])
axarr[2].set_xlabel('t, s')
# draw vertical lines
axarr[2].plot([0.6985, 0.6985], [-4800, 2000], 'r-', lw=1)
axarr[2].plot([0.6985+0.008, 0.6985+0.008], [-4800, 2000], 'r-', lw=1)
axarr[2].annotate(
    s='',
    xy=(0.6985,-4000),
    xytext=(0.6985+0.008,-4000),
    arrowprops=dict(arrowstyle='<->'))
axarr[2].annotate(
    s='período de\n   pitch',
    xy=(0.7005,-3700))
axarr[2].axis('tight')
plt.show()

Um método simples de se estimar a frequência de pitch, $F_0$ , e por isso nem sempre muito eficiente, é pela função de autocorrelação. Abaixo apresenta-se a função de autocorrelação e sua aplicação a um trecho selecionado do sinal da página anterior. Dado um trecho de $N$ amostras do sinal $x(n)$, sua autocorrelação, $R(n)$, pode ser dada por:

$$ R(k) = \sum_{n=0}^{N-k-1} x(n+k) \; x(n), \;\; k=0, 1, 2, \ldots, N-1 $$

Calculada a autocorrelação, basta agora determinar o valor de $n$ onde $R(n)$ é máxima após os valores iniciais. Esse processo pode ser feito automaticamente, contudo, da figura, nota-se que esse valor de $n$ vale 65. Lembrando que a frequência de amostragem do sinal seis.wav é 8 kHz, chega-se a $$ F_0 = \frac{8000}{65} \approx 123 \text{ Hz} $$ que corresponde aproximadamente ao valor estimado anteriormente para o mesmo trecho de sinal.

In [51]:
# trecho da análise anterior
s = seis[ind]
N = len(s)
R = np.zeros(N)
for k in range(N):
    R[k] = sum(s[k:N]*s[0:N-k])

R = R/np.max(R)
offset = 10
xm = np.argmax(R[offset:])
ym = np.max(R[offset:]) # lembrar que media foi subtraida do sinal
xm += offset
print('xm =', xm, '\nym =', ym)
plt.figure(figsize=(10,8))
plt.plot(R)
plt.title('autocorrelação')
plt.ylabel('$R(k)$', fontsize=18)
plt.xlabel('$k$', fontsize=18)
plt.grid()
msg = 'X: ' + str(xm) + '\nY: ' + str(ym)
plt.annotate(msg, xy=(xm, ym), xytext=(100, 0.8),
             arrowprops=dict(facecolor='red', shrink=0.01))
plt.axis('tight')
plt.show()

xm = 65 
ym = 0.711048956561

Formantes

As formantes são as frequências de ressonância do trato vocal. Por exemplo, para cada vogal o trato vocal assume uma configuração relativamente estável, determinando frequências de ressonância específicas para cada vogal. A figura ilustra a relação entre a primeira, $F_1$, e a segunda, $F_2$, formantes para vogais da língua inglesa.

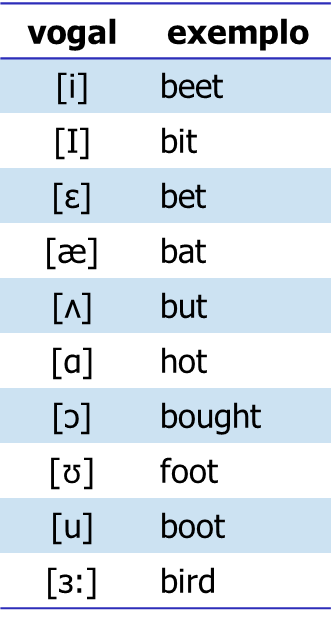
Vogais e consoantes

Abaixo é apresentado o exemplo de uma vogal. Note a quase periodicidade do sinal devido à vibração das cordas vocais. Processou-se esse trecho pela técnica de predição linear e compararam-se os espectros obtidos pela FFT e pelos coeficientes de predição linear (LPC). Note que esta última técnica ressalta as ressonâncias do trato vocal, permitindo uma melhor análise das frequências formantes.

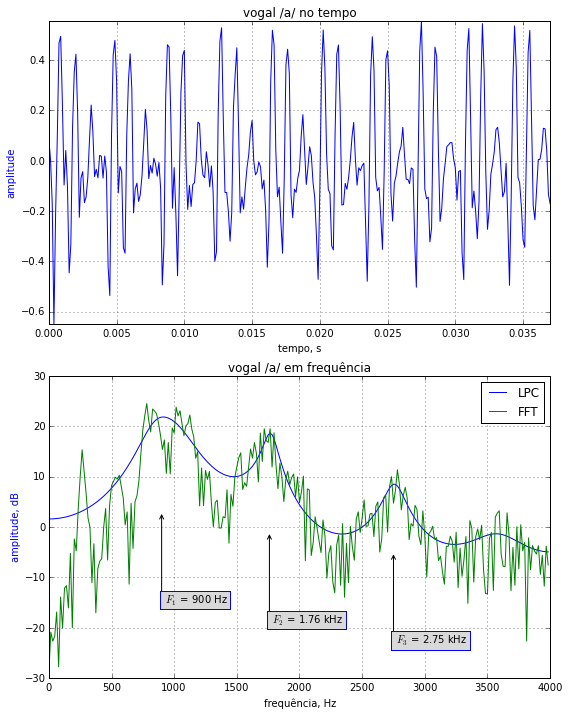
Da figura:

$$ \begin{eqnarray} F_1 & \approx & 0.90 \text{ kHz} \\ F_2 & \approx & 1.76 \text{ kHz} \\ F_3 & \approx & 2.75 \text{ kHz} \end{eqnarray} $$

Compare com os valores para essa vogal no gráfico $F_1 \times F_2$ anterior.

Abaixo é apresentado um exemplo de uma consoante. Consoantes podem ser sonoras, quando há vibração das cordas vocais, e surdas, quando não há vibração das cordas vocais. Abaixo é apresentada uma consoante surda, como o 'ch' de 'chá'. Note o aspecto de ruidoso desse sinal no tempo e que a concentração de energia do sinal se encontra em frequências relativamente mais altas, sem existir um claro padrão de presença de formantes.

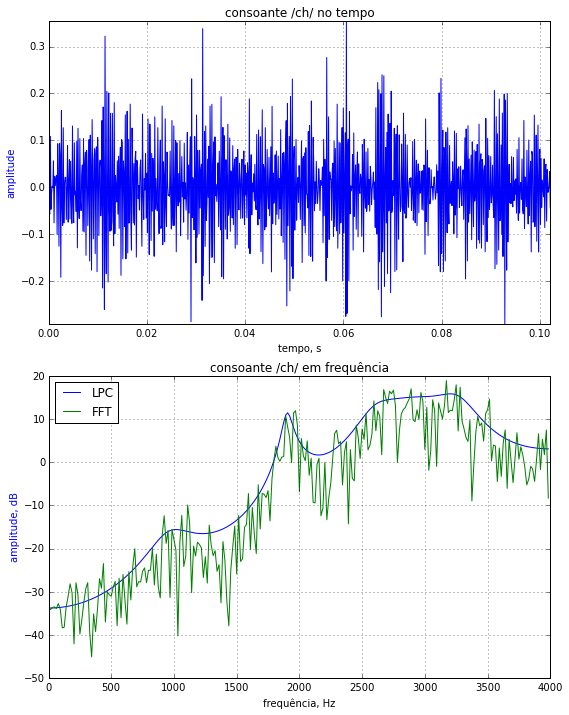
Abaixo é apresentada uma consoante sonora, como o 'z' de 'zê'. Note que existe uma periodicidade no sinal, devido à vibração das cordas vocais. O espectro tem um comportamento razoavelmente plano quando comparado aos dois exemplos anteriores.

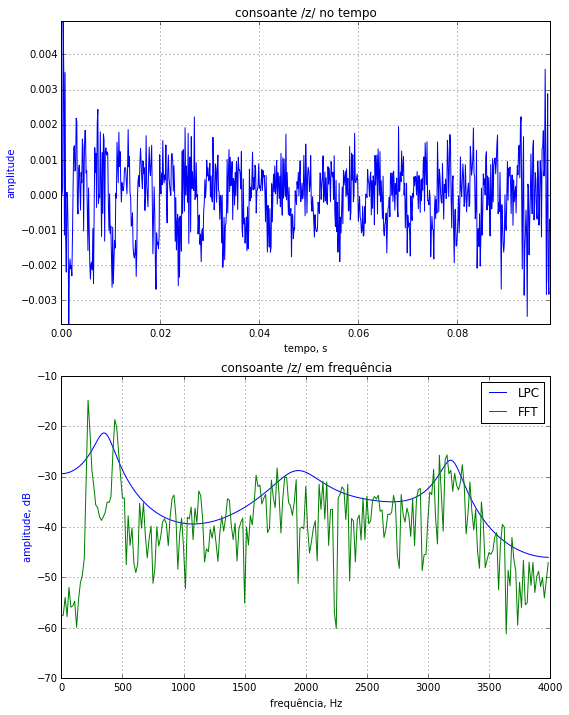
Curvas de loudness

(Fletcher-Munson, Equal Loudness Curves for Pure Tones, 1933)

A sensibilidade auditiva varia com a frequência do tom. Note a maior sensibilidade para tons em 3.5 kHz

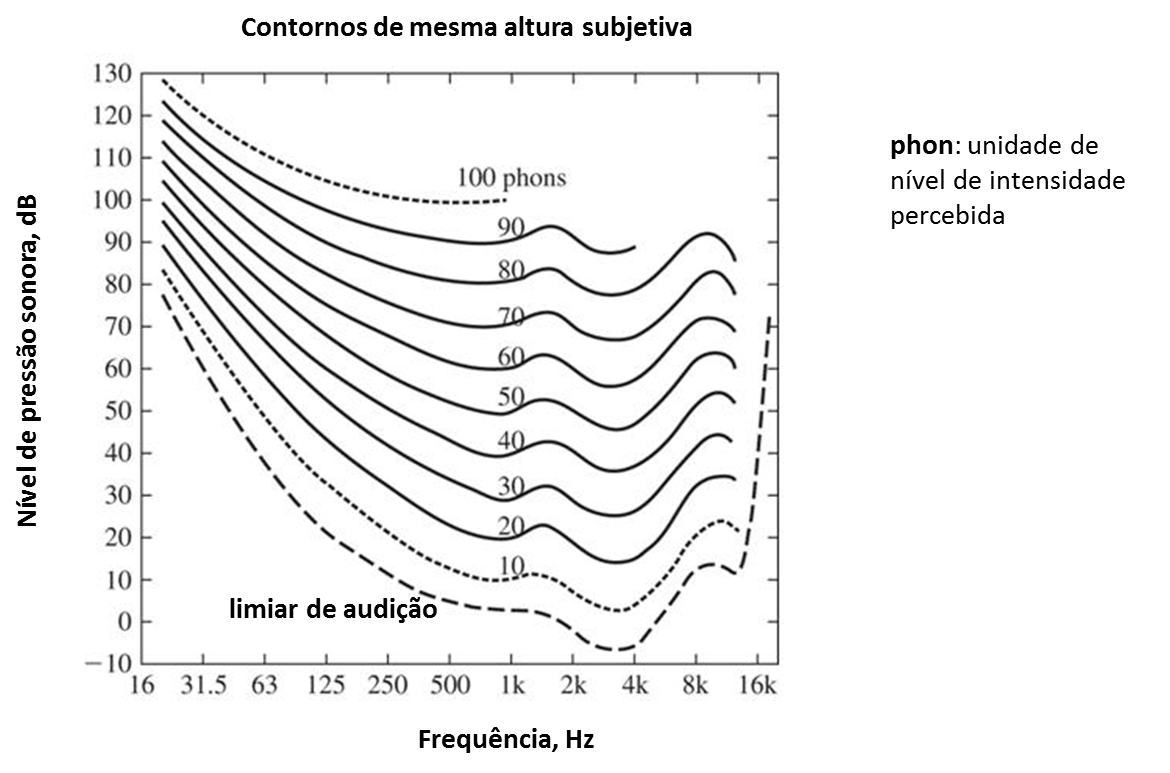
Use a função genlin(), definida anteriormente, para testar sua percepção com alguns tons:

T  = 5 # duração em s
fs = 44100
f1 = 3500 # freq. tom 1
s1 = genlin(T, f1, f1, fs)
f2 = 250 # freq. tom 2
s2 = genlin(T, f2, f2, fs);
# etc.

Bandas críticas

O termo banda crítica é usado de diversas formas na literatura. Originalmente foi usado por Fletcher (1940) com respeito ao mascaramento de um tom por ruído branco. Investigava-se quanto do ruído branco era responsável para o mascarameto do tom. Em outras palavras, o objetivo era determinar se toda a banda espectral do ruído contribuía para mascarar o tom ou se há uma certa banda espectral limitada, ou "banda crítica", do ruído que já bastava para o mascaramento completo. Foi descoberto que apenas uma banda crítica, centralizada na frequência do tom já era suficiente para o mascaramento. Note, pela tabela a seguir, que:

  • Baixas frequências têm-se bandas mais estreitas (filtros mais seletivos)
  • Altas frequências têm-se bandas menos estreitas (filtros menos seletivos)


No Freq. Central, Hz Larg. de Banda, Hz
1 50 80
2 150 100
3 250 100
4 350 100
5 450 110
6 570 120
7 700 140
8 840 150
9 1000 160
10 1170 190
11 1370 210
12 1600 240
No Freq. Central, Hz Larg. de Banda, Hz
13 1850 280
14 2150 320
15 2500 380
16 2900 450
17 3400 550
18 4000 700
19 4800 900
20 5800 1100
21 7000 1300
22 8500 1800
23 10500 2500
24 13500 3500

Notar o comportamento exponencial/logarítmico das bandas críticas em função da frequência

In [52]:
# bandas críticas
fc  =  [50, 150, 250, 350, 450, 570, 700, 840, 1000, 1170, 1370, 1600, 1850, 2150,\
        2500, 2900, 3400, 4000, 4800, 5800, 7000, 8500, 10500, 13500]
bw  =  [80, 100, 100, 100, 110, 120, 140, 150, 160, 190, 210, 240, 280, 320, 380,\
        450, 550, 700, 900, 1100, 1300, 1800, 2500, 3500]
N = len(fc)

f, ax = plt.subplots(2, 1, figsize=(12,10))

for i in range(N):
    fi = fc[i]
    di = bw[i]/2
    df = bw[i]
    ax[0].plot([fi-df, fi-di, fi-di/2, fi+di/2, fi+di, fi+df], [0, .7, 1, 1, .7, 0]);
    ax[1].semilogx([fi-df, fi-di, fi-di/2, fi+di/2, fi+di, fi+df], [0, .7, 1, 1, .7, 0]);

ax[0].set_xlim([0.1, 18000])
ax[0].set_ylim([0, 1.05])
ax[0].set_title('Bandas críticas (frequência escala linear)')
ax[0].set_xlabel('f, Hz')
ax[0].grid()
ax[1].set_xlim([50, 18000])
ax[1].set_ylim([0, 1.05])
ax[1].set_title('Bandas críticas (frequência escala logarítmica)')
ax[1].set_xlabel('f, Hz')
ax[1].grid()
plt.show()

Mascaramento

Um sinal mais fraco é completamente mascarado por um sinal mais intenso com conteúdo similar em frequência (próximo em termos de banda crítica). Este fenômeno é convenientemente empregado na codificação mp3 de forma a comprimir a informação pela eliminação de tons perceptuais desnecessários.

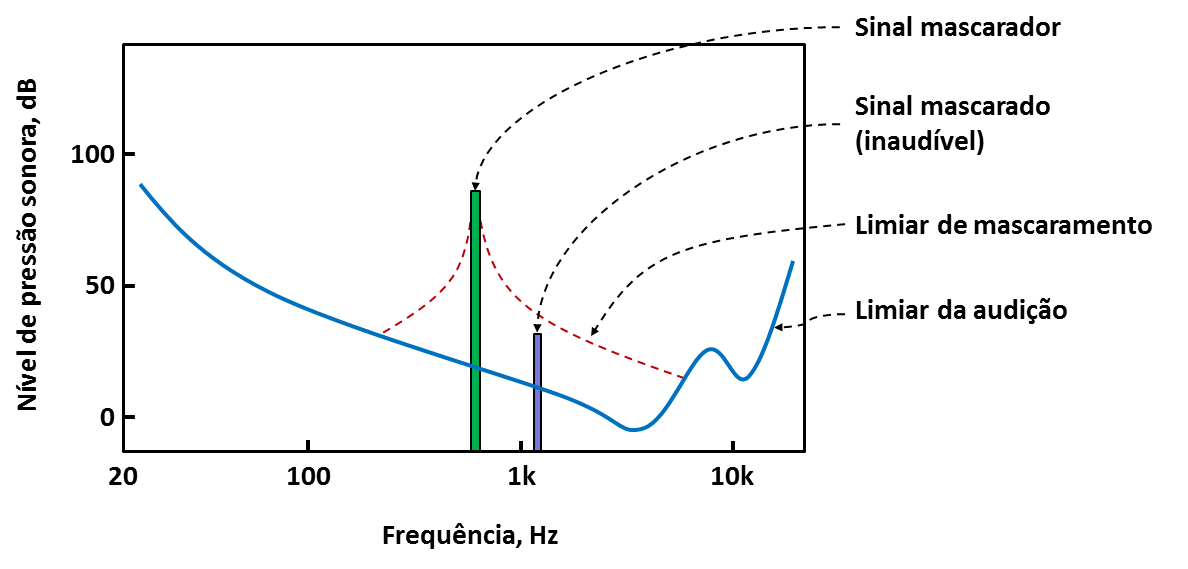
Use a função genlin(), definida anteriormente, para testar o mascaramento:

T  = 5 # duração em s
fs = 44100
f1 = 800  # freq. tom 1
s1 = genlin(T, f1, f1, fs)
f2 = 1100 # freq. tom 2
s2 = genlin(T, f2, f2, fs)
s3 = (s1 + 5e-2 * s2)*0.9
# escutar e comparar s1, s2 e s3

Algumas aplicações

  • Microphone array - filtragem espacial e localização de fontes sonoras
  • Reconhecimento automático de fala
  • Autenticação de locutor – biometria
  • TTS (text-to-speech) - síntese de voz em leitura de textos
  • Voice morphing - modificação de voz
  • Codificação - representação mais eficiente para transmissão/armazenam.
  • Speech enhancement - redução de ruído
  • Aplicações em música – análise/transformação de música/canto
  • Estimação de faixa etária/sentimento/stress

Algumas referências bibliográficas

  • L.R. Rabiner and R.W. Schafer. Theory and Applications of Digital Speech Processing. Prentice-Hall; 2010
  • A.V. Oppenheim, R.W. Schafer. Discrete-Time Signal Processing. 3rd edition. Prentice Hall. 2011
  • L.R. Rabiner and B.H. Juang. Fundamentals of Speech Recognition. Prentice Hall; 1993
  • X. Huang, A. Acero and H.W. Hon. Spoken Language Processing: A Guide to Theory, Algorithm and System Development. Prentice Hall; 2001
  • P. Taylor. Text-to-Speech Synthesis. Cambridge University Press; 2009
  • I.J. Tashev. Sound Capture and Processing. John Wiley; 2009

Exercícios de laboratório

Geração de tom (cossenoide)

Transformar os passos descritos anteriormente na geração de tom na frequência f1 em uma função em Python, como descrita abaixo:

def geracos(A, f1, ph, fs, T):
   """
   Entradas:
      A : amplitude desejada
      f1: frequência desejada para o tom, Hz
      ph: fase, rad
      fs: frequência de amostragem para reprodução, Hz
      T : duração, s
   Saída:
      tom: sinal com as características dos parâmetros acima
           A * cos(2 * pi * f1 * n / fs + ph), n = 0, 1, ..., T * fs
   """

Nota: para padronizar, usar função cosseno, cos()

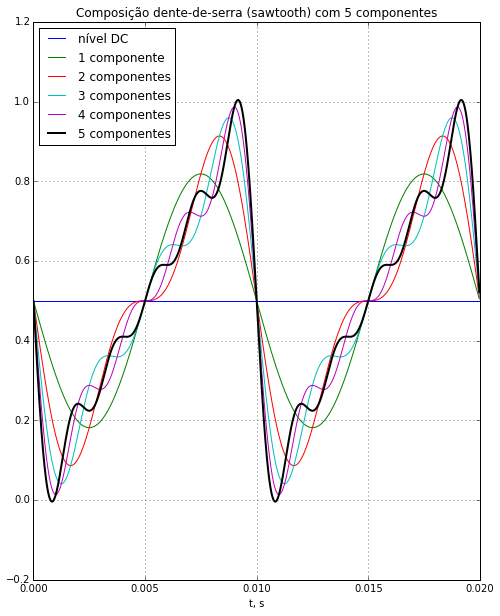
Geração de tom (teste com série de Fourier)

Se a sua implementação do gerador de tom cossenoidal, como descrito anteriormente, estiver correta e gerar o tom esperado, o seguinte código gerará a composição via série de Fourier da sequência dente-de-serra (sawtooth)

fs = 44100 # freq amostragem, Hz
f1 = 100 # freq fundamental, Hz
T = 2 # duracao, s
N = np.floor(fs/f1) # pontos por periodo
n = np.arange(T*fs) # indice das amostras
t = n/fs # escala de tempo, s
C = 5 # no. componentes para serie
P = 2 # no. de periodos para visualizacao
ind = np.arange(P*N, dtype=int) # indice eixo x para visualizacao

s = geracos(1/2, 0, 0, fs, T) # nivel DC
plt.plot(t[ind], s[ind])
for i in range(1, C+1): # soma C componentes a s
    s = s + geracos(1/np.pi/i, i*f1, np.pi/2, fs, T)
    plt.plot(t[ind], s[ind])

plt.plot(t[ind], s[ind], 'k', linewidth=2)
msg = 'Composição dente-de-serra (sawtooth)'
msg =  msg + ' com {0} componentes'.format(C)
plt.title(msg)
plt.xlabel('t, s');
plt.grid()
plt.show()

Posteriormente, varie o número de componentes, C, e experimente a geração de outras formas de onda

Introdução de eco

Iremos a seguir criar um novo sinal composto por ecos do sinal original, no caso o sinal de voz do arquivo seis.wav. A ideia é simplesmente somar repetições do mesmo sinal atrasadas pelos intervalos de eco desejado. Isso é facilmente feito pela convolução do sinal original por um trem de impulsos, como descrito a seguir. Reproduza os passos abaixo e escute o sinal resultante. Entenda e varie a receita abaixo para poder controlar os intervalos de eco, assim como as amplitudes dos sinais ecoados.

import winsound
from scipy.io import wavfile
fname = 'seis.wav'
fsseis, seis = wavfile.read(fname)
seis = seis / 2**15 # sinal entre -1 e 1
T = 0.6 # echo em s
A = 0.8 # atenuacao do echo
K = 14  # quantidade de echoes
N = int(T * fsseis) # pontos por periodo de echo
trem = np.zeros(N*(K+1))
trem[0] = 1
for i in range(K): # K echoes
    trem[(i+1)*N] = trem[i*N] * A

out = np.convolve(seis, trem)
t = np.arange(len(out))/fsseis
plt.plot(t, out)
plt.grid()
plt.title('sinal com ecos')
plt.xlabel('t, s')
plt.axis('tight')
plt.show()

# para ouvir:
# fname = 'echoes.wav'
# samples = out.astype(np.short)
# wavfile.write(fname, fsseis, samples)
# winsound.PlaySound(fname, winsound.SND_FILENAME)

Inversão no tempo

Importe as amostras do arquivo seis.wav e escute-as de trás para frente. Crie um novo arquivo, sies.wav, com as amostras invertidas no tempo.

Dica: entenda o código abaixo

sieis = seis[-1::-1]
plt.plot(sieis)
plt.title('seis invertido no tempo')
plt.grid()
plt.show()

# para ouvir:
fname = 'sies.wav'
samples = sieis * 2**15
samples = samples.astype(np.short)
wavfile.write(fname, fsseis, samples)
winsound.PlaySound(fname, winsound.SND_FILENAME)

Áudio estéreo

Crie um arquivo estereo.wav de 2 canais (estéreo) no qual em um canal se tem um tom que varia sua frequência linearmente de 100 Hz a 22 kHz em 5 segundos e no outro canal um tom que varia linearmente de 22 kHz a 100 Hz em 5 segundos. Use procedimentos análogos aos apresentados anteriormente. Adote frequência de amostragem de 44100 Hz.

Espectrograma da soma dos sinais:

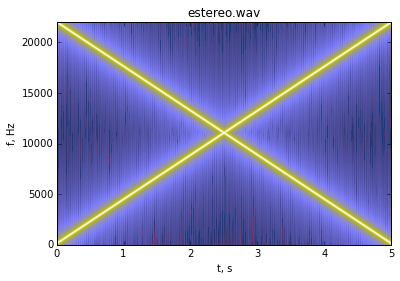
Redução do ruído no sinal senoidal com SNR = 5 dB

Reproduza o processo de filtragem realizado anteriormente para outras especificações de filtro: teste ordens e frequências diferentes.

Energia e taxa de cruzamentos por zero (TCZ)

Dado o arquivo de áudio seis.wav, compute a energia, $E$, e a TCZ, $Z$, desse sinal em segmentos de 20 ms a cada 10 ms.

Passos:

  1. De acordo com a notação usada anteriormente, determine $T$, $S$, $dS$, $M$ e $N$
  2. Retire o nível médio do sinal (apenas recomendação geral, pois o sinal em questão já teve seu nível médio removido)
  3. Entre em um loop, que sabemos terá $M$ passadas, e para cada passada $i$ compute a energia do segmento $i$, $E(i)$, e a correspondente taxa de cruzamentos por zero, $Z(i)$.
  4. Apresente os gráficos de $E$ e $Z$. Deve resultar nos gráficos vistos quando foram abordados os conceitos de segmentação, energia e TCZ.

Função de autocorrelação

Implemente a função de autocorrelação e chegue à mesma figura de $R(n)$ apresentada anteriormente. Para se chegar ao mesmo gráfico, obviamente, use o mesmo trecho de sinal usado anteriormente.

Dica: faça x = y[ind], como no código correspondente, e trabalhe com x para a reprodução do gráfico de $R(n)$ , após sua implementação.